Использование данных и конфиденциальность данных часто противоречат друг другу. Например, если мы все открыто поделимся данными о своем здоровье с исследователями, это ускорит работу над новыми технологиями и лекарствами для здоровья. Но мы справедливо опасаемся того, что злоумышленник может сделать с нашими необработанными данными о состоянии здоровья. Вот где на помощь может прийти криптография. Повторное шифрование через прокси и гомоморфное шифрование — это инструменты, которые позволят нам сохранить свой пирог и съесть его, когда дело доходит до использования данных и конфиденциальности данных.
Повторное шифрование через прокси-сервер позволяет владельцу данных один раз зашифровать свои данные, а затем безопасно делиться ими с покупателями так часто, как они того пожелают, используя услуги третьей стороны. Гомоморфное шифрование позволяет покупателю данных выполнять вычисления с зашифрованными данными, которые хранятся и вычисляются ненадежными третьими сторонами, и получать результаты или аналитические данные по этим данным, не раскрывая при этом данные какого-либо лица в незашифрованном виде.
Эти методы служат строительными блоками более сложных криптосистем (например, Unlynx разработан EPFL, теоретическим вдохновением для нашей текущей работы). Таким образом, наш план таков 1) создавать простые в использовании и практичные библиотеки для передовых криптографических примитивов 2) эти библиотеки помогут разработчикам создавать и комбинировать передовые примитивы для создания сложных криптосистем, которые обеспечат более безопасный обмен данными. 3) Более безопасный и полезный обмен данными позволит в 10 раз быстрее исследовать такие важные проблемы, как исследования рака и диабета. 4) спасти мир :-).
Для начала мы разработали альфа-версию экспериментальной версии библиотека . В приведенном ниже коде эта библиотека используется, чтобы предложить пример того, как мы применяем эти технологии для обеспечения безопасного и удобного потока данных от владельцев к пользователям.
Повторное шифрование через прокси
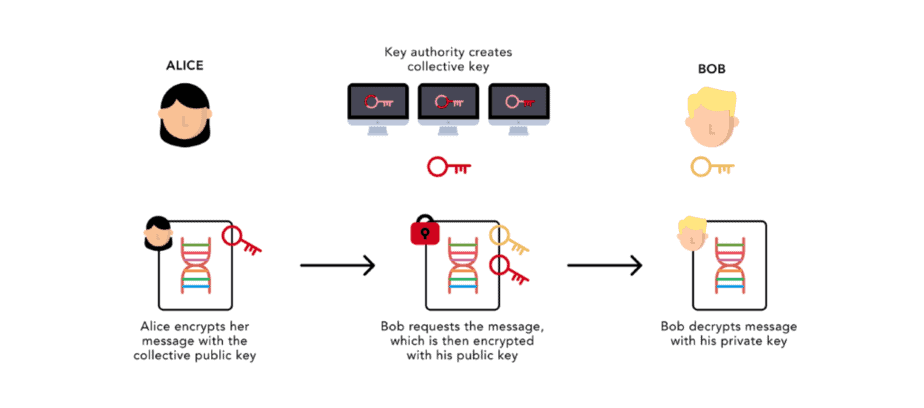
Повторное шифрование с помощью прокси — это процесс, в котором третья сторона, называемая прокси, изменяет зашифрованный текст, зашифрованный одной стороной, таким образом, что он может быть расшифрован второй стороной.
На платформе Nebula прокси будет действовать как хранитель зашифрованных геномных данных и управлять доступом покупателей к этим данным от имени владельца. Хотя прокси-сервер не может получить доступ к исходным необработанным данным, он может (с разрешения владельца) изменять зашифрованные данные, чтобы пользователь мог впоследствии их расшифровать. Таким образом, владелец данных может делегировать эту задачу прокси-серверу, не передавая прокси-сервера никакой информации в виде открытого текста. Еще одним следствием этого делегирования является то, что ни владелец данных, ни получатель не должны находиться в сети.
В нашем примере предположим, что прокси — это набор серверов, которые действуют как децентрализованный коллективный орган. Теперь давайте рассмотрим пример повторного шифрования через прокси, где Алиса, владелец данных, делится геномными данными с Бобом, пользователем данных, через прокси.
Сначала установим указанную выше библиотеку.

Теперь мы можем импортировать пакет nebula.

Теперь давайте пройдемся по процессу обмена. Первый шаг для Алисы — зашифровать свои данные. Мы создадим для нее симметричный ключ, который будет использовать ChaCha20 + Poly1305 .

(<umbral.point.Point at 0x10389fe10>, b'\x10\x91Y\xb1*\x8c\xf0\x7f@=\xefx\xe9\xf6\x12\xf3W\xbd\xdel\xc4\x06{\xae\x05%\x1b\x89U\xf9eN\xe5e\x1a\xe71xn\xac@v\xf4')Прокси-сервер коллективного управления имеет свой собственный открытый ключ, который представляет собой сумму открытых ключей составляющих его серверов.
Теперь Алиса берет ключ шифрования, который она использовала для своих данных, и шифрует его открытым ключом коллективного органа. Обратите внимание: поскольку мы используем криптография с эллиптической кривой два зашифрованных текста, которые Шифрование Эль-Гамаля производит точки на выбранной эллиптической кривой. В выводе ниже вы видите координаты двух точек в форме (x, y).

((35632791306511153190425382918654119432212363349182003014749353343128802126727, 64242079364444117954338938658093117507689717419524224721788857406414950009581), (97847103734799578346073884785318736156070617710068604497289838935308031857554, 100772267217308028038724925681024365362775942293927562577198462564518506731626))Каждый сервер в коллективной власти частично расшифровывает, а затем повторно шифрует ключ Алисы для Боба.
- Чтобы частично расшифровать ключ Алисы, каждый сервер использует свой закрытый ключ.
- Чтобы частично повторно зашифровать ключ Алисы для Боба, каждый сервер использует открытый ключ Боба.

((77420738395268270953686214496801457604160876120513979866307802146750959593560, 54288930850798967899941066319180759019666461705141800680259295043110704970240), (43931260115404950504844368880031328989231014591201216806426924428987149667105, 90907867688890000833998990379245369153741769092073562236593684729778667077837))Боб получает и затем расшифровывает ключ Алисы, используя свой закрытый ключ, а затем использует ключ Алисы для расшифровки исходных данных.

True
b'My genomic data'Только представьте себе здесь полный геном, а не только эту строку!
Гомоморфное шифрование
Шифрование Эль-Гамаля аддитивно гомоморфный , что означает, что результат суммирования зашифрованных текстов отражает результат, который был бы получен при суммировании соответствующих открытых текстов. Из-за этого, если мы расшифруем зашифрованную сумму, результатом будет сумма открытых текстов. Гомоморфное шифрование позволяет заинтересованной стороне запросить агрегированную информацию и получить соответствующий ответ, но без просмотра базовых точек данных. (Предполагается, что соблюдаются некоторые другие ограничения, как указано Вот .)
Ниже приведен трехэтапный пример, показывающий, как наш коллективный орган власти / доверенное лицо может ответить на запрос Боба о количестве людей с определенным вариантом гена в нашем наборе данных.
- Орган выполняет необходимые вычисления для зашифрованных данных в наборе данных.
- Власть берет этот совокупный результат (люди отмечаются 1 за наличие варианта и 0 за его отсутствие) и повторно шифрует его открытым ключом Боба.
- Боб расшифровывает совокупный результат с помощью своего закрытого ключа и теперь имеет правильную сумму, но не видит отдельные точки данных.
Суммирование зашифрованных данных
Ниже мы «моделируем» 1000 человек, предоставляющих платформе геномную информацию. Всего 448 человек с этим вариантом гена. Данные каждого человека зашифрованы и надежно хранятся.

Number of people withвариант гена: 488 ((21226922480075498561329291252368547521899161064631964196023720750821691033728, 22373176000434530074330330136750061845273006440607485558527039957320386973412), (73527396063873421512162165532068395819931745318640280343429662961367630577212, 38439465994848418879243894553165852646308170673055923181635051985961737087067))
CA повторно зашифровывает зашифрованную сумму для Боба
Боб идет дальше и запрашивает информацию о частоте вариантов гена в популяции. CA суммирует и повторно шифрует данные Бобу. Обратите внимание, что координаты (x, y) повторно зашифрованного шифра не равны координатам исходного шифра выше.

((26066336990521229606715532856762274058860058654632118019680516577894483977430, 111016076743629331281471026942315236039952684121365861080441162051376755931177), (74777752915141648361212288792719003318012040162755253888817602184232651456038, 79121323403285772024091404265686004833455157263244527767410139385386809682035))Боб расшифровывает сумму

(488, 488)Боб может получить представление о данных в целом, не углубляясь в информацию о каком-либо отдельном владельце. Это позволяет владельцам данных, которые не хотят раскрывать свои данные, по-прежнему вносить свой вклад в платформу.
Обратите внимание, что повторное шифрование через прокси-сервер сыграло ключевую роль в обеспечении удобства для Боба. Поскольку каждый владелец данных делегировал полномочия прокси-серверу, Бобу нужно было выполнить только один запрос. Без прокси-сервера ему пришлось бы запрашивать каждую точку данных, которую он хотел.
Повторное шифрование с помощью прокси и гомоморфное шифрование помогают Nebula защищать данные пользователей, обеспечивать удобный доступ к данным для покупателей данных и позволяют покупателям данных генерировать аналитические данные без ущерба для личной конфиденциальности.
Призыв к действию
В Nebula Genomics мы считаем, что проблемы конфиденциальности являются серьезным препятствием для обмена биомедицинскими данными. Это препятствует медицинским исследованиям и разработке новых методов лечения. Мы не можем решить эту задачу в одиночку.
Если вас интересует код, не стесняйтесь играть с библиотекой, но будьте осторожны: эта конкретная реализация не прошла аудит безопасности и в настоящее время предназначена только для образовательного использования 🙂
Если вы хотите узнать больше о геномике туманностей, обязательно Следуйте за нами на Twitter чтобы оставаться в курсе.