Data use and data privacy are often in conflict. For example, if we all openly shared our health data with researchers, it would speed up work on new health technologies and cures. But we are rightly afraid of what a malicious actor could do with our raw health data. That is where the field of cryptography can come to the rescue. Re-encryption by proxy and homomorphic encryption are tools that will allow us to keep our cake and eat it too, when it comes to data use and data privacy.
Re-encryption by proxy allows a data owner to encrypt their data once, and subsequently share it securely with buyers, as often as they wish, using the services of a third party. Homomorphic encryption allows a data buyer to run computations on encrypted data stored and computed on by untrusted third parties, and obtain results or insights on that data, while not revealing any individual’s data in unencrypted form.
These techniques serve as the building blocks of more complex crypto systems (for example Unlynx developed by EPFL, the theoretical inspiration for our current work). Thus our plan is as follows 1) build out simple to use and practical libraries for advanced cryptography primitives 2) these libraries will help developers create and combine advanced primitives to create complex crypto systems that will allow more secure data sharing 3) More secure and useful data sharing will 10x the speed of research on important problems like cancer and diabetes research 4) save the world :-).
To start off we’ve developed an alpha version of a proof-of-concept library. The code below uses that library to offer an example of how we apply those technologies to enable a secure and convenient data flow from owners to users.
Re-encryption by Proxy
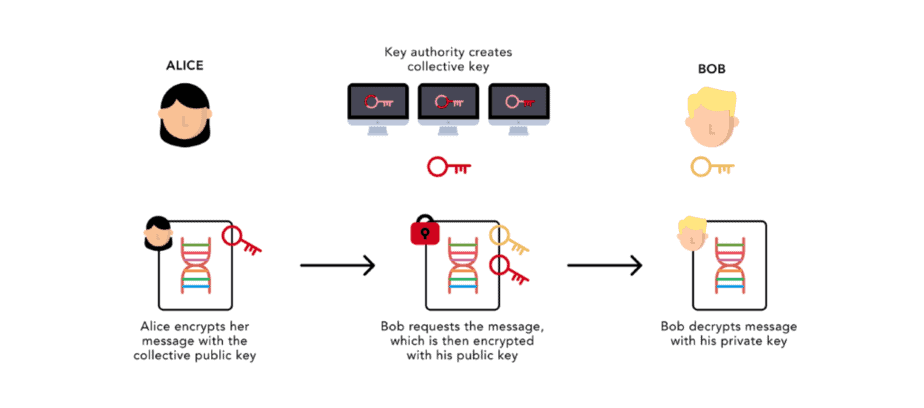
Re-encryption by proxy is a process in which a third party, called the proxy, alters a ciphertext encrypted by one party in such a way that it may be decrypted by a second party.
On Nebula’s platform, the proxy will act as a custodian for encrypted genomic data and manage access to that data by buyers on behalf of the owner. While the proxy cannot access the underlying raw data, the proxy is able (with the permission of the owner) to modify the encrypted data so that the user can subsequently decrypt it. The data owner is thus able to delegate this task to the proxy while never sharing any plaintext information with the proxy. Another consequence of this delegation is that neither the data owner nor recipient need to be online.
In our example, assume the proxy is a set of servers that acts as a decentralized collective authority. Now, let’s walk through an example of re-encryption by proxy where Alice, a data owner, shares genomic data with Bob, a data user, via the proxy.
First let’s install the library mentioned above.

Now we can import the nebula package.

Now, let’s walk through the sharing process. The first step is for Alice to encrypt her data. We’ll generate a symmetric key for her to be used by ChaCha20+Poly1305.

(<umbral.point.Point at 0x10389fe10>, b'\x10\x91Y\xb1*\x8c\xf0\x7f@=\xefx\xe9\xf6\x12\xf3W\xbd\xdel\xc4\x06{\xae\x05%\x1b\x89U\xf9eN\xe5e\x1a\xe71xn\xac@v\xf4')The collective authority proxy has its own public key, which is the sum of the public keys of its constituent servers.
Alice now takes the encryption key she used on her data, and encrypts it with the collective authority’s public key. Note that since we’re using elliptic-curve cryptography the two ciphertexts that ElGamal encryption produces are points on the chosen elliptic curve. What you see in the output below are the coordinates of the two points in (x, y) form.

((35632791306511153190425382918654119432212363349182003014749353343128802126727, 64242079364444117954338938658093117507689717419524224721788857406414950009581), (97847103734799578346073884785318736156070617710068604497289838935308031857554, 100772267217308028038724925681024365362775942293927562577198462564518506731626))Each server in the collective authority partially decrypts, then re-encrypts Alice’s key for Bob.
- To partially decrypt Alice’s key, each server uses its private key
- To partially re-encrypt Alice’s key for Bob, each server uses Bob’s public key

((77420738395268270953686214496801457604160876120513979866307802146750959593560, 54288930850798967899941066319180759019666461705141800680259295043110704970240), (43931260115404950504844368880031328989231014591201216806426924428987149667105, 90907867688890000833998990379245369153741769092073562236593684729778667077837))Bob receives and then decrypts Alice’s key using his private key, then uses Alice’s key to decrypt the original data.

True
b'My genomic data'Just imagine a full genome here instead of just this string!
Homomorphic Encryption
ElGamal encryption is additively homomorphic, meaning that the result of summing ciphertexts mirrors the result that would be obtained from summing the corresponding plaintexts. Because of this, if we decrypt an encrypted sum, the result will be the sum of the plaintexts. Homomorphic encryption allows an interested party to issue a query for aggregated information and obtain the relevant answer but without seeing the underlying data points. (This assumes some other constraints are met, as specified here.)
Below is a three step example showing how our collective authority/proxy could answer a query from Bob about the number of people with a particular gene variant in our dataset.
- The authority performs the necessary computation on the encrypted data in the dataset.
- The authority takes this aggregate result (people are marked 1 for having the variant and 0 for not having it)and re-encrypts it with Bob’s public key.
- Bob decrypts the aggregate result with his private key, and now has the correct sum but no visibility of the individual data points.
Summing encrypted data
Below we “simulate” 1000 people providing genomic information to the platform. In total there are 448 people with this particular gene variant. Each person’s data is encrypted and stored securely.

Number of people withgene variant: 488 ((21226922480075498561329291252368547521899161064631964196023720750821691033728, 22373176000434530074330330136750061845273006440607485558527039957320386973412), (73527396063873421512162165532068395819931745318640280343429662961367630577212, 38439465994848418879243894553165852646308170673055923181635051985961737087067))
CA re-encrypts encrypted sum for Bob
Bob goes ahead and requests information about the gene variant frequency in the population. The CA sums it up and re-encrypts the data to Bob. Notice that the (x, y) coordinates of the re-encrypted cipher are not equal to coordinates of the original cipher above.

((26066336990521229606715532856762274058860058654632118019680516577894483977430, 111016076743629331281471026942315236039952684121365861080441162051376755931177), (74777752915141648361212288792719003318012040162755253888817602184232651456038, 79121323403285772024091404265686004833455157263244527767410139385386809682035))Bob decrypts sum

(488, 488)Bob is able to gain insight into the data as a whole without gaining insight into any individual owner’s information. This allows data owners who don’t want to reveal their data to still contribute to the platform.
Notice that re-encryption by proxy played a key role in making this convenient for Bob. Because each data owner delegated to the proxy, Bob only needed to issue one query. Without the proxy he would need to issue a query for every data point he wanted.
Re-encryption by proxy and homomorphic encryption help Nebula secure user data, provide convenient access to data for data buyers, and allow data buyers to generate insights without compromising individual privacy.
Call to Action
At Nebula Genomics we believe that privacy concerns are a significant hurdle to biomedical data sharing. This hinders medical research and development of new treatments. We can’t solve this challenge alone.
If you are interested in the code, feel free to play with the library, but be safe: this particular implementation hasn’t undergone a security audit and is currently for educational use only 🙂
If you’re interested in exploring more about Nebula Genomics in particular, make sure to follow us on twitter to stay up to date.